Bitwise operation과 Java의 BigInteger에 대하여 알아보고 다른 부가적인 것들에 대해서도 정리해 보겠다.
Bitwise operation(비트 연산)이란 한 개 또는 두 개의 이진수에 대해 비트 단위로 적용되는 연산이다.
비트 연산의 종류로는 AND 연산, OR 연산, XOR 연산, NOT 연산 그리고 SHIFT 연산들이 있다.
● AND 연산
- 두 값의 각 자릿수를 비교해, 두 값 모두에 1이 있을 때에만 1을, 나머지 경우에는 0을 계산하는 연산이다.
비트 A(= 0101)와 B(= 1100)가 있을 때, "A & B" 로 표현하며 0100의 결과를 만들어낸다.

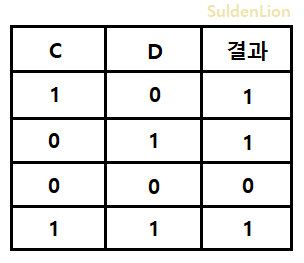
● OR 연산
- 두 값의 각 자릿수를 비교해, 둘 중 하나라도 1이 있다면 1을, 아니면 0을 계산하는 연산이다.
비트 C(= 1001)와 D(= 0101)이 있을 때, "C | D"로 표현하며 1101의 결과를 갖는다.
● XOR 연산
- 두 값의 각 자릿수를 비교해, 값이 같으면 0, 다르면 1을 계산하는 연산이다.
비트 X(= 0011)와 Y(= 0101)이 있을 때, "X ^ Y"로 표현하며 0110의 결과를 갖는다.

● NOT 연산
- NOT 연산은 한 개의 비트 Z(= 1000)이 있을 때, 각 자릿수의 값을 반대로 바꾸는 연산이다.
"~Z"로 표현하며 이의 결과로는 0111이 된다.

● SHIFT 연산
- 왼쪽으로 1비트씩 이동하는 "<<"와 오른쪽으로 1비트씩 이동하는 ">>" 두 가지 연산이 있다.
A(= 0101 1100)라는 비트가 있을 때, "A << 3"은 왼쪽으로 3비트 이동하라는 연산이며 1110 0000이 그 결과이다.
반대로 "A >> 3"은 오른쪽으로 3비트 이동이며 0000 1011이 연산 결과이다.
비트 연산을 알아야 하는 이유는 비트 마스크(Bit Mask)의 사용에 있는데 이에 대해 알아보겠다.
▶ 비트마스크 (BitMask)
정수의 이진수 표현을 활용한 기법이다.
우리가 Keyboard를 통해 타이핑하여 컴퓨터에 어떤 정보를 입력하려 한다. 하지만 Keyboard 값을 입력받을때
한 바이트씩밖에 입력받지 못한다 (ab를 치고 싶을때 a 따로 b 따로 치는것이지 ab가 동시에 쳐지는 것이 아닌 것과 같다). 하지만 우리는 두 개 이상의 키보드 자판을 눌러서 특수 글자를 치거나 특정한 일을 수행하곤 한다. (ex. "Ctrl + Alt + Delete", "Alt + F4", a의 대문자 입력을 위한 "Shift + a" 등..)

전하고자하는 내용과 다를 수 있지만 차후에 보기위한 메모
이런 식의 미리 정의된 Keyboard 값들의 조합의 개수는 무지막지하게 많을 것이다. 컴퓨터 기록 자원은 무한하지 않으므로 이러한 문제를 해결하기 위해 고안된 것이 비트마스크이다.
자료형(Data type)을 잠시 보겠다.프로그램에서의 자료란 메모리상의 어떠한 공간에 기록된 데이터들을 의미한다. 자료형은 일련의 메모리 공간에 의미를 부여하는 방법이다.int라는 자료형은 "2의 31승 -1 (= -2147483648)부터 2의 31승 (= 2147483648) "의 데이터만큼 메모리상에 원하는 공간을 예약할 수 있다. ※ 2의 32승이 아닌 이유는 맨 첫번째 자리 비트 하나를 음수인지 양수인지 판별하기 위해 사용했기 때문이다. → unsigned int 키워드를 사용하면 부호가 없는 변수임을 표기하며, 2의 32승(= 0 ~ 4294967296)까지 표현할 수 있다.
이 unsigned int를 이용하여 비트마스크를 사용할 것이고 다음과 같은 예제에서 쓰일 것이다.

Java API의 InputEvent에 대한 내용을 발췌하였다.
프로그램을 만들면서 Accelerator와 같은 keyEvent를 줄 경우가 자주 있는데, 그럴때 보통 ALT_DOWN_MASK, CTRL_DOWN_MASK, SHIFT_DOWN_MASK를 사용하곤 한다.
비트마스크의 장점으로는 크게 수행시간이 빠르다는 것, 짧은 코드로 구현된다는 것, 적은 메모리를 사용한다는 것을 들 수 있다. 비트마스크 연산은 bit 단위 연산이기에 O(1)로 구현되는 경우가 많다. 따라서 다른 자료구조를 이용하는 것보다 훨씬 빠를 수 있다. 하지만 비트의 개수만큼 원소를 다룰 수 있기 때문에 연산 횟수가 적은 경우는 속도가 별 차이가 없지만 연산 횟수가 늘어날수록 속도 차이가 커지게 된다. 그리고 비트마스크 연산은 다양한 집합 연산들을 Bitwise operation으로 한 줄로 작성 가능하기 때문에 반복문, 조건문 등을 이용한 코드보다 간결하게 작성할 수 있다. 또한 0과 1의 두가지 경우를 가지는 각 bit들은 2^n 가지의 경우를 n bit 2진수 하나로 표현이 가능하다. 이는 곧 하나의 정수로 매우 많은 경우의 수를 표현할 수 있기 때문에 메모리 측면에서 효율적이며, 더 많은 데이터를 미리 계산해서 저장해 둘 수 있는 장점을 가진다.
비트마스크를 만들어보겠다.

매크로로 Alt, Function, Ctrl, Shift를 위한 마스크를 정의해준다.
이건 2진수로 다음처럼 정의된 것과 같다.

이제 읽거나 쓸 숫자가 들어오면 각 마스크가 맡고있는 위치의 2진 숫자와 상황에 맞는 연산을 한다.

Masking을 할 때 두가지 케이스로 나누어야 하는데, 어떤 수를 read하여 그 수가 마스킹이 되어 있는가 확인하는 용도의 연산과 write를 하려는데 어떤 Mask로 마스킹을 할 것인가의 연산으로 나뉜다.
unsigned int k(= 000...001010)가 있고 CTRL_MASK가 되어있는가를 구한다고 가정해보겠다.
if (k & CTRL_MASK) {
...
}소스 코드상에선 이런식으로 조건문을 세울 것이고 & 작업을 수행한다.

해당 마스크의 값 (CTRL_MASK = 0 1 0 0)과 k를 비교하는데, 두 값 모두에 1이 있을 때에만 1, 나머지 경우에는 0이므로 비교하는 위치가 아닌 위치는 모조리 0이 되고, 들어오는 수의 해당 자리가 1이라면 1, 0이라면 0이 된다.
그로인해 읽어오는 이 k가 CTRL_MASK가 되어있는가를 판단할 수 있다.
이제 쓰기의 경우인데, k의 내용을 변경(삽입)하려는 경우이다. k가 CTRL_MASK를 갖도록 해보겠다.
k = k | CTRL_MASK;
두 비트중 하나라도 1이면 1인 OR 연산을 사용한다.

나머지 자리는 값을 건드리지 않고 마스킹이 필요한 위치만 변경한다.
다음도 쓰기의 경우인데, k의 내용을 변경(삭제)하는 경우이다. k가 갖고있는 SHIFT_MASK(4번째 위치)를 없애려면 어떻게 해야되는지 보겠다.
k = k & (~ SHIFT_MASK)일단 SHIFT_MASK의 내용을 2's complement화 한다.
SHIFT_MASK의 내용은 000...01000 인데 이를 2의 보수화 하면 111...10111이 될 것이다.
이 상태에서 k와 & 작업을 하면 k의 SHIFT_MASK에 해당하는 내용을 걷어낼 수 있을 것이다.

2진수 자리들의 값이 둘 다 1일 경우에만 1이 되기 때문에 연산하면

000 ... 000010과 같이 SHIFT_MASK에 해당하는 마스킹이 제거된 값을 얻을 수 있다.
비트마스크는 위와 같은 방식으로 하면 된다.
추가로 가볍게 Is power of 2에 대해 알아보겠다.
연구실 동생 조광일이가 북아메리카 면접내용에 있다고 말해준 내용이다. 어떤 수가 2의 n승인지 O(1)로 판단할 수 있는 법을 알아내는 것이다.
이것도 Bitwise operation으로 풀어낼 수 있다.
어떤 수 x가 있을 때, x와 x-1을 &한 값이 0과 같으면 그 수는 2의 n제곱승이다. (x값이 0이 아니라는 조건에서)
예를 들어, x가 16일 때)

16과 15를 한 값이 0이 되므로 16은 2의 n제곱승이다.
만약 x가 19일 때)

결과 값이 0이 아니므로 2의 n제곱승이 아니다.
마지막으로, Bitwise 연산을 통해 swap연산하는 것을 알아보겠다.
우리는 보통 어떤 값 a와 b가 있을 때, a에 b의 내용을 넣고 b에 a의 내용을 넣고 싶다면 임시변수 tmp를 둬서 하나씩 옮기는 식으로 swap한다.
int a = 8;
int b = 3;
int tmp;
tmp = a;
a = b;
b = tmp;하지만 이런 방법보다 코드도 간결하고 임시 변수 tmp를 만들지 않고 swap하는 방법이 있다.
바로 a와 b만으로 XOR 연산을 이용해 구하는 방법이다.
a = a ^ b를 하고 b = b ^ a를 한 후, a = a ^ b를 하는 세 가지 단계만 거치면 a에는 b의 내용이 담기고 b에는 a의 내용이 담기게 될 것이다.


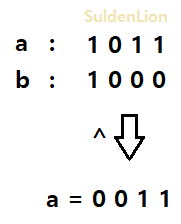
다음과 같이 a에는 0011(= 3), b에는 1000(= 8)의 값이 담기게 되는 것을 확인할 수 있다.
그리고 이 작업을 코드상에서 극단적으로 짧게 나타낸다면
a^=b^=a^=b이렇게 표현도 가능하다.
댓글