BigInteger의 구현 원리를 알아보고 C++로 만들어 보도록 하겠다.
메모리 상에 표현가능한 정수의 범위로는 2의 32승 만큼인 -2,147,483,648 ~ +2,147,483,647이다.
하지만 실생활에선 21억이 넘어가는 숫자를 사용할 일이 충분히 많이 있다.
이런 경우에 사용하기 위해서 자릿수 제한 없이 정수 숫자를 표현할 수 있는 BigInteger에 대해 알아보고 만들어 보겠다.
BigInteger는 데이터로 들어온 숫자를 문자열로 취급하여 표현할 것이다.
BigInteger x;
BigInteger y("-1234");
BigInteger z(y);
x = "1234";BigInteger 변수 선언시 생성자에 문자열이 parameter로써 들어가거나 다른 BigInteger의 값을 가지고 변수에 값을 저장하는 일이 일반적이게 될 것이다.
데이터 변수로는 char * 타입의 digit와 int size를 가질 것이다.
그리고 입력받은 숫자가 양수이냐 음수이냐에 따라 BigInteger에 숫자 setting 방식이 구분될 것이다.
BigInteger x에 "1234"를 세팅해 준다고 가정해 보겠다.
strlen("1234")의 결과 4에 1을 더한만큼의 크기를 가진 배열을 생성해준다.
배열의 0번 인덱스에는 양수임을 확인하기 위한 0을 넣어주고, 각 자리 숫자를 차례로 배열에 넣어준다.
동적으로 이 숫자를 다루기 위한 작업이다.

반면 음수를 BigInteger에 세팅한다면 어떻게 해야 할까
숫자로만 표기될 digit 배열에 '-'를 넣을 수도 없는 노릇이다.
하지만 "음수를 양수처럼", "뺄셈을 덧셈처럼" 사용할 수 있는 방법이 있다.
바로 Ten's complement라는 개념이 사용될 것이다.
(Ten's complement = Nine's complement + 1 // To find 9's complement subtract each and every decimal digit from 9)
바로 사용 예를 보여주겠다.
BigInteger y에 "-1234"를 넣는다고 가정해 본다.
digit 배열의 크기는 -1234의 length와 같다.
가장 앞자리수 1앞에 9를 넣어준다. 여기서 9는 '-' 기호를 의미하는 것과 같다.
그리고 각 자리에서 (9 - 각 자리에 있는 수)를 한 값을 배열에다 담아준다.

그 다음 이 배열의 값에 +1을 하면 10의 보수화가 완료된다.

(01234가 0001234로 표현해도 상관없듯이, 98766을 999998766으로 표현하는 것은 같다.)
constructor에서 이런식으로 char * type으로 오거나 BigInteger type으로 오는 값을 setting 해주면 된다.

이렇게 선언된 변수들을 가지고 operator overloading을 한 덧셈, 뺄셈, 곱셈, 나눗셈 연산을 하도록 할 것이다.
먼저 덧셈을 하는 경우이다.
덧셈이 모든 연산에 있어서 핵심적인데, 뺄셈, 곱셈, 나눗셈의 모든 연산들도 결국 덧셈을 통해 구현되어지기 때문이다.
"379" 라는 숫자와 "2380"이라는 숫자를 더한다고 가정해보겠다. (양수끼리의 덧셈)
두 수는 문자열 형태로 들어오고 각 자리 숫자를 덧셈하기 좋게 맞춰준다.

this에 해당하는 BigInteger와 피연산자 BigInteger operand를 둔다.
연산을 하기 위해선 두 수가 모두 Plus인지 혹은 모두 Minus인지, 아니면 두 개가 각각 Plus와 Minus 인지를 확인해준다.
두 수가 모두 양수거나 음수일때는 maxLength를 두 수중 더 큰 사이즈에 +1로 정해준다. (연산 과정에서 최대 자릿수에 carry가 발생할 수 있기 때문)
두 수의 부호가 다른 경우는 maxLength를 두 수중 더 큰 사이즈의 값으로 지정해준다.
그 다음 this에 해당하는 BigInteger와 operand라는 BigInteger를 maxLength 크기의 BigInteger로 다시 선언해준다.

maxLength 6의 size 배열을 선언하고 원래 BigInteger가 갖고있던 기호(맨 앞 인덱스의 숫자)로 배열 전체를 초기화 시켜준다. (음수라면 9로 배열전체가 초기화됨)
배열 뒤에서부터 실제 값들을 채워넣어주고 두 수를 더해줄 것이다.
result를 기준으로 accumulateNumber(data2)를 시행한다.
맨 뒤 인덱스부터 차례대로 각 수를 더하며 더한수가 10을 넘어가면 carry를 발생시킨다. 그리고 해당 자리는 10을 뺀 나머지 숫자를 넣고 그 다음 자릿수는 각각의 value와 carry를 더한 값을 넣는 작업을 반복한다.
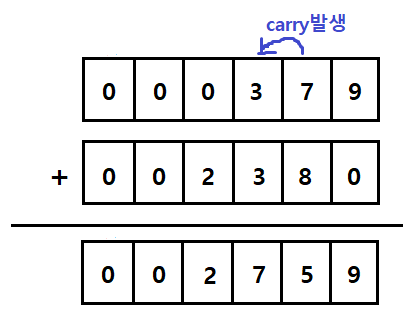
계산이 완료되면 result는 아래와 같이 남게 된다.
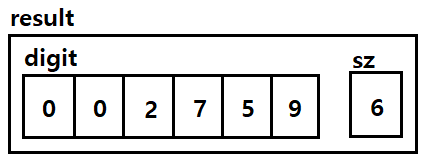
이 상태에서 반복되는 0(또는 9)를 걷어내는 작업을 해준다.
size 값에서 맨 앞 인덱스 숫자와 중복된 0(또는 9)의 수를 뺀 만큼의 버퍼를 dynamic allocation으로 하나 만들어주고 값들을 뒤에서부터 모조리 옮긴다.
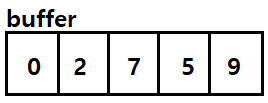
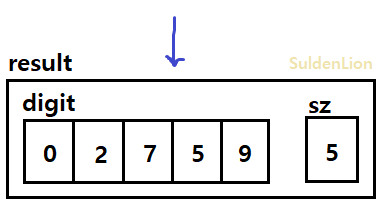
result의 digit을 buffer로 갈아끼워주면 덧셈 작업이 마무리된다.
다음은 뺄셈을 하는 경우이다.
"26" - "8835"를 해보겠다.
이는 양수 26과 음수 -8835의 덧셈과 같다. 즉, 26과 Ten's complement된 -8835인 91165를 더하는 것과 같다.
뒤에 있는 피연산자의 부호를 바꾸는 작업을 convertSign이라고 하겠다.
data "8835"의 맨 앞자리가 '-'라면(-8835라면), data+1에 해당하는 부분부터 strdup를 해주면 '-'만 걷어내고 8835로 변환한다.
data "8835"의 맨 앞에 '-'가 없다면, 사이즈가 data의 길이 + 2한 만큼의 char *를 만들어주고 맨 앞 인덱스에 '-'를 붙여준다. 그리고 p+1 부터 data 값들을 strcpy 해주고 p를 리턴시켜주면 "-8835\0"이 넘어올 것이다.
이렇게 변환된 값들로 '+' 작업을 해준다.
"26" + "91165" => "91191"이 될 것이고, 이를 10's complement하여(=8808) +1을 해준 후 '-'를 붙여주면(= -8809) 원하는 답이 나올 것이다.
곱셈의 경우를 보겠다.
"-45"와 "763"의 수를 곱해보겠다.
곱셈할때 두 수가 모두 양수거나 음수이면 결과값이 양수, 둘중 하나라도 음수라면 결과값이 음수이다.
숫자만 곱셈을 해주고 위의 규칙에 따라 부호를 붙여주면 된다.
곱셈도 +연산을 통해 구현하는 것인데, 피연산자 하나와 다른 피연산자의 각 자리에 있는 수를 이용해 더해주는 방법이 있다.
그림으로 보겠다.
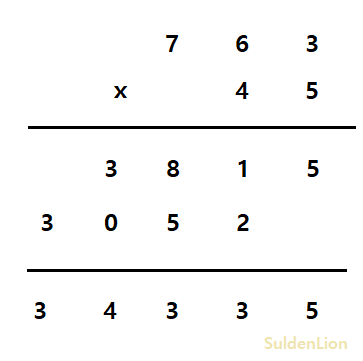
일반적으로 노트에 곱셈을 한다면 위의 방식으로 구할 것이다.
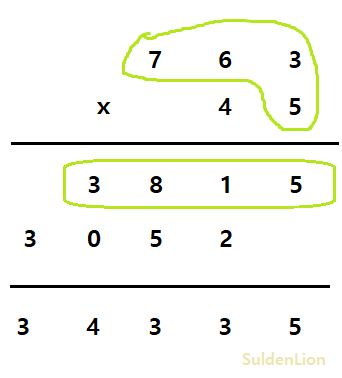
3815의 값은 763 * 5를 한 과정의 값이고
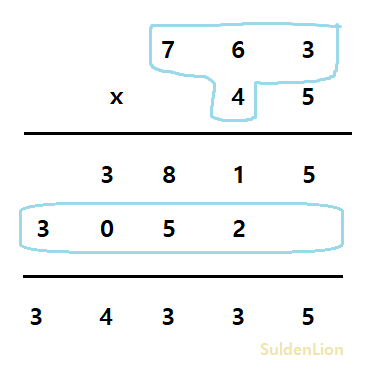
30520에 해당하는 값은 763 * 40을 하는 과정의 값과 같다.
이 두수를 더하고 '-'를 씌워주면 원하는 결과가 나오는 것이다.
위 내용은 즉, (763이라는 숫자를 3번 더한 것) + (763이라는 수를 40번 더한 것)과 같다.
이를 효율적으로 더할 수 있게 표현하면 (763을 3번 더한 것) + (7630을 4번 더한 것)으로 표현가능하다.
'-'만 씌워주면 "-34335"로 연산 완료.
ex) 12345 * 98765 = (12345 * 5) + (123450 * 6) + (1234500 * 7) + (12345000 * 8) + (123450000 * 9)
이렇게 연산하면 숫자가 아무리 커도 속도면에서 크게 느리지 않게 곱셈 연산을 할 수 있다.
마지막으로 나눗셈이다.
곱셈과 같이 두 수가 모두 +나 -이면 +의 결과를, 아닌 경우는 -의 결과를 갖는다.
길이가 큰 쪽에서 짧은 쪽으로 뺄셈 작업을 하면 되는데,
길이가 짧은 숫자의 길이만큼 길이가 큰 숫자의 길이를 앞에서 부터 빼가며 몫을 구한다.
"-7490" / "-70"의 연산을 해보겠다.
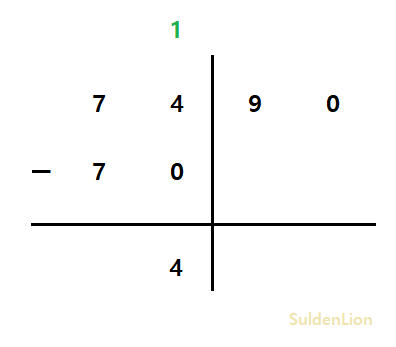
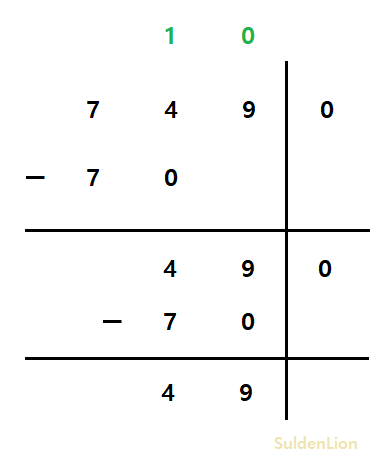
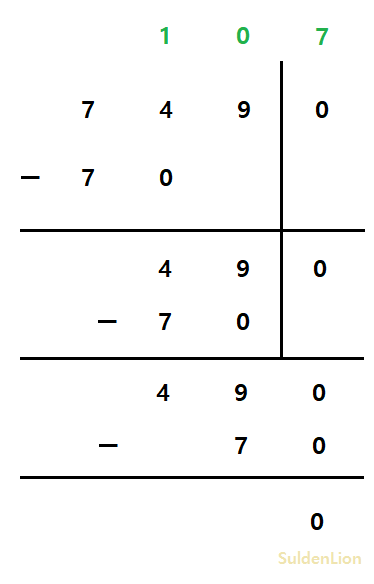
뺄셈 작업을 하면 위와 같이 몫을 도출해낼 수 있다. 뺼셈은 위에서 만들어 놓은 것을 이용하면 될 것이다.
아래는 BigInteger 구현 코드이다.
#include <iostream>
using namespace std;
#include <string.h>
class BigInteger {
char *digit;
int sz;
void set(const char *data);
void set(BigInteger &data);
int plusOne();
char *createStringWhenPlus();
char *createStringWhenMinus();
static char *convertSign(const char *data);
void setDigitsFromPlusString(const char *data);
void setDigitsFromMinusString(const char *data);
static bool isPlus(const char *data);
bool isPlus();
int accumulateNumber(BigInteger &data);
void trimSign();
bool equalsZero();
void shiftLeft();
public:
BigInteger();
BigInteger(const char *data);
BigInteger(BigInteger &data);
BigInteger(int n,const char *data);
BigInteger(int n,BigInteger &data);
BigInteger(int n);
~BigInteger() {
delete digit;
}
char *toString();
void operator=(const char *data);
void operator=(BigInteger &data);
BigInteger operator+(const char *data);
BigInteger operator+(BigInteger &data);
BigInteger operator-(const char *data);
BigInteger operator-(BigInteger &data);
BigInteger operator*(const char *data);
BigInteger operator*(BigInteger &data);
BigInteger divide(const char *data);
bool operator>(const char *data);
bool operator>(BigInteger &data);
bool operator<(const char *data);
bool operator<(BigInteger &data);
bool operator==(const char *data);
bool operator==(BigInteger &data);
bool operator>=(const char *data);
bool operator>=(BigInteger &data);
bool operator<=(const char *data);
bool operator<=(BigInteger &data);
friend ostream& operator<<(ostream &out,BigInteger &num);
};
BigInteger::BigInteger() {
set("0");
}
BigInteger::BigInteger(const char *data)
{
set(data);
}
BigInteger::BigInteger(BigInteger &data)
{
set(data);
}
BigInteger::BigInteger(int n)
{
sz = n;
digit = new char[n];
for(int i = 0; i < sz; i++) {
digit[i] = 0;
}
}
BigInteger::BigInteger(int n,const char *data)
{
sz = n;
digit = new char[n];
for(int i = 0; i < sz; i++) {
digit[i] = 0;
}
int j = sz - 1;
for(int i = strlen(data)-1; i >= 0; i--) {
digit[j] = data[i] - '0';
j--;
}
}
BigInteger::BigInteger(int n,BigInteger &data)
{
sz = n;
digit = new char[n];
for(int i = 0; i < sz; i++) {
digit[i] = data.digit[0];
}
int j = sz - 1;
for(int i = data.sz-1; i >= 0; i--) {
digit[j] = data.digit[i];
j--;
}
}
void BigInteger::set(BigInteger &data)
{
sz = data.sz;
digit = new char[sz];
for(int i = 0; i < sz; i++) digit[i] = data.digit[i];
}
bool BigInteger::operator>(const char *data)
{
BigInteger tmp;
tmp = (*this) - data;
if (tmp.isPlus()) return true;
return false;
}
bool BigInteger::operator>(BigInteger &data)
{
char *s = data.toString();
return *this > s;
}
bool BigInteger::operator<(const char *data)
{
BigInteger tmp;
tmp = (*this) - data;
if (tmp.isPlus()) return false;
return true;
}
bool BigInteger::operator<(BigInteger &data)
{
char *s = data.toString();
return *this < s;
}
void BigInteger::operator=(const char *data)
{
set(data);
}
void BigInteger::operator=(BigInteger &data)
{
set(data);
}
bool BigInteger::isPlus()
{
if (digit[0] == 0) return true;
else return false;
}
bool BigInteger::isPlus(const char *data)
{
if (*data == '-') return false;
else return true;
}
void BigInteger::trimSign()
{
if (sz <= 2) return;
int signCount = 1;
for(int i = 1; i < sz; i++) {
if (digit[i] == digit[0]) signCount++;
else break;
}
if (signCount == 1) return;
char *buf = new char[sz - signCount + 1];
int j = sz - signCount;
for(int i = sz-1; i >= signCount-1; i--) {
buf[j] = digit[i];
j--;
}
sz = sz - signCount + 1;
digit = buf;
}
int BigInteger::accumulateNumber(BigInteger &data)
{
int carry = 0;
for (int i = sz-1; i >= 0; i--) {
digit[i] = digit[i] + data.digit[i] + carry;
if (digit[i] >= 10) {
digit[i] = digit[i] - 10;
carry = 1;
} else {
carry = 0;
}
}
return carry;
}
char *BigInteger::convertSign(const char *data)
{
if (*data == '-') {
return strdup(data+1);
} else {
char *p = new char[strlen(data) + 2];
*p = '-';
strcpy(p+1,data);
return p;
}
}
BigInteger BigInteger::operator-(BigInteger &data)
{
char *s = data.toString();
return (*this) - s;
}
BigInteger BigInteger::operator-(const char *data)
{
char *operand = convertSign(data);
return *this + operand;
}
BigInteger BigInteger::operator+(BigInteger &data)
{
char *s = data.toString();
return (*this) + s;
}
bool BigInteger::equalsZero()
{
for (int i = 0; i < sz; i++) {
if (digit[i] != 0) return false;
}
return true;
}
bool BigInteger::operator==(const char *data)
{
BigInteger tmp;
tmp = (*this) - data;
if (tmp.equalsZero()) return true;
return false;
}
bool BigInteger::operator>=(const char *data)
{
return ((*this)>data || (*this)==data);
}
bool BigInteger::operator>=(BigInteger &data)
{
return ((*this)>data || (*this)==data);
}
bool BigInteger::operator<=(const char *data)
{
return ((*this)<data || (*this)==data);
}
bool BigInteger::operator<=(BigInteger &data)
{
return ((*this)<data || (*this)==data);
}
bool BigInteger::operator==(BigInteger &data)
{
char *s = data.toString();
return (*this) == s;
}
void BigInteger::shiftLeft()
{
for (int i = 1; i < sz; i++) {
digit[i-1] = digit[i];
}
digit[sz-1] = 0;
}
BigInteger BigInteger::operator*(BigInteger &data)
{
char *s = data.toString();
return (*this) * s;
}
BigInteger BigInteger::operator*(const char *data)
{
BigInteger operand(data);
int resultSign = 0; // 0 : plus 1 : minus
if ((isPlus() == true && operand.isPlus() == true) ||
(isPlus() == false && operand.isPlus() == false)) {
resultSign = 0;
} else {
resultSign = 1;
}
char *data1 = toString();
char *data2 = operand.toString();
if (isPlus(data1) == false) {
data1 = convertSign(data1);
}
if (isPlus(data2) == false) {
data2 = convertSign(data2);
}
int maxLength = sz + operand.sz - 1;
BigInteger result(maxLength);
BigInteger addum(maxLength,data1);
BigInteger count(data2);
//cout << "&&&" << result << " " << addum << " " << count << endl;
/*while(!count.equalsZero()) {
result.accumulateNumber(addum);
count = count - "1";
cout << "result = " << result << "\n";
}*/
int countSize = count.sz - 1;
for (int i = countSize; i > 0; i--) {
for (int j = 0; j < count.digit[i]; j++) {
result.accumulateNumber(addum);
}
addum.shiftLeft();
}
result.trimSign();
if (resultSign == 1) {
char *plusResult = result.toString();
char *minusResult = convertSign(plusResult);
return BigInteger(minusResult);
} else {
return result;
}
}
BigInteger BigInteger::divide(const char *data)
{
BigInteger operand(data);
int resultSign = 0; // 0 : plus 1 : minus
if ((isPlus() == true && operand.isPlus() == true) ||
(isPlus() == false && operand.isPlus() == false)) {
resultSign = 0;
} else {
resultSign = 1;
}
char *data1 = toString();
char *data2 = operand.toString();
if (isPlus(data1) == false) {
data1 = convertSign(data1);
}
if (isPlus(data2) == false) {
data2 = convertSign(data2);
}
BigInteger numerator(data1);
BigInteger denominator(data2);
BigInteger result(sz, "0");
while (numerator >= denominator) {
numerator = numerator - denominator;
result = result + "1";
}
result.trimSign();
if (resultSign == 1) {
char *plusResult = result.toString();
char *minusResult = convertSign(plusResult);
return BigInteger(minusResult);
} else {
return result;
}
return result;
}
BigInteger BigInteger::operator+(const char *data)
{
BigInteger operand(data);
int maxLength = 0;
int sz1 = sz;
int sz2 = operand.sz;
if ((isPlus() == true && operand.isPlus() == true) ||
(isPlus() == false && operand.isPlus() == false)) {
if (sz1 > sz2) maxLength = sz1 + 1;
else maxLength = sz2 + 1;
} else {
if (sz1 > sz2) maxLength = sz1;
else maxLength = sz2;
}
BigInteger result(maxLength,*this);
BigInteger data2(maxLength,operand);
result.accumulateNumber(data2);
result.trimSign();
return result;
}
char *BigInteger::createStringWhenPlus()
{
char *buf = new char[sz];
for(int i = 1; i < sz; i++) {
buf[i-1] = digit[i] + '0';
}
buf[sz-1] = '\0';
return buf;
}
char *BigInteger::createStringWhenMinus()
{
char *buf = new char[sz+1];
buf[0] = '-';
for(int i = 1; i < sz; i++) {
buf[i] = 9 - digit[i];
}
int carry = 1;
for(int i = sz-1; i > 0; i--) {
if (carry == 0) break;
buf[i] = buf[i] + carry;
if (buf[i] >= 10) {
buf[i] = buf[i] - 10;
carry = 1;
} else {
carry = 0;
}
}
buf[sz] = '\0';
for(int i = 1; i < sz; i++) {
buf[i] = buf[i] + '0';
}
return buf;
}
char *BigInteger::toString()
{
if (isPlus()) {
return createStringWhenPlus();
} else {
return createStringWhenMinus();
}
}
void BigInteger::setDigitsFromPlusString(const char *data)
{
int len = strlen(data);
sz = len + 1;
digit = new char[len+1];
digit[0] = 0;
for (int i = 1; i < len+1; i++) {
digit[i] = data[i-1] - '0';
}
}
int BigInteger::plusOne()
{
int carry = 1;
for(int i = sz-1; i >= 0; i--) {
if (carry == 0) break;
digit[i] = digit[i] + carry;
if (digit[i] >= 10) {
digit[i] = digit[i] - 10;
carry = 1;
} else {
carry = 0;
}
}
return carry;
}
void BigInteger::setDigitsFromMinusString(const char *data)
{
int len = strlen(data);
sz = len;
digit = new char[len];
digit[0] = 9;
for (int i = 1; i < len; i++) {
digit[i] = 9 - (data[i] - '0');
}
plusOne();
}
void BigInteger::set(const char *data)
{
if (BigInteger::isPlus(data)) {
setDigitsFromPlusString(data);
} else {
setDigitsFromMinusString(data);
}
}
ostream& operator<<(ostream &out,BigInteger &num)
{
char *s = num.toString();
out << s;
return out;
}
void main()
{
BigInteger x;
BigInteger y("-1234");
BigInteger z(y);
x = "1234";
y = "33";
// z = x + "65";
z = x + y;
x = "999";
y = "9999";
z = x * y;
/*if (x > "1") {
cout << "greater than" << endl;
} else {
cout << "less than" << endl;
}*/
x = "2300";
z = x.divide("3");
cout << x << ", " << y << ", " << z << endl;
}
(곱셈 작업에서는 shiftLeft()라는 함수로 자리수를 효율적으로 처리하게 했으나 나눗셈은 귀찮은 관계로 하지 않음)
'Algorithm' 카테고리의 다른 글
| K번째수_프로그래머스 (0) | 2024.02.29 |
|---|---|
| bitCount 메서드 사용 (다음 큰 숫자_프로그래머스) (0) | 2024.02.20 |
| Algorithm - Merge Sort (병합 정렬) (0) | 2022.08.18 |
| Algorithm - Sieve of Eratosthenes(소수판별 알고리즘) (0) | 2022.07.30 |
| Algorithm - 크루스칼 알고리즘(Kruskal) (0) | 2022.07.21 |

댓글