ㆍ 대수학
- 대수학이란 수학 문제를 간단하게 만드는 기술들, 미지수에 변수를 대입하는 기술, 그리고 이를 계산하는 기술. (방정식을 푸는 기술)
- 고전의 대수학은 명칭 그대로 수를 대신해 문자를 사용하는 방법으로 방정식을 푸는 방법을 연구하는 학문에서 시작됨.
- 19세기 이후 에바리스트 갈루아가 대수방정식(Algebraic equation)을 연구하기 위해 군이라는 대수적 구조를 도입했고, 이후 현대에서는 고전과는 다르게 추상화되었으며, 방정식의 해법은 대수방정식론이라는 대수학의 일부분이 됨.
ㆍ 대수방정식
- 대수방정식이란 어떤 변수를 대수식(덧셈, 뺄셈, 곱셈, 나눗셈, 거듭제곱 등)으로만 표현된 대수함수 f(x)를 f(x)=0의 식으로 나타낸 것을 말함
- 즉, 대수방정식의 가장 간단한 형태는 다항식.
- 이차방정식, 삼차방정식, 사차방정식 등이 대수방정식이라고 할 수 있음
ㆍ 선형대수학
- 선형대수학은 선형방정식을 풀기 위한 수학적인 도구로써, 기하학의 문제를 효과적으로 해결하기 위한 방법론으로부터 시작되었으며, 지금은 공학/자연과학/사회과학/경제학 등의 응용에 매우 중요한 역할을 담당하고 있음.
- 특히 선형대수학 이론은 전기회로, 통신 네트워크, 동역학, 선형계획법, 컴퓨터 그래픽, 기상예보 등 수많은 분야에서 매우 중요한 자리를 차지함
▷ 현대사회의 선형대수학 적용 분야
- 교통흐름, 전기회로에서 kirchhof 전류법칙과 더불어 특정 지점의 전류값 측정, 화학에서 화학방정식의 성립.
- leontief 경제모델, 경제분야에서의 선형 계획법, 생태학에서 leslie 모델, 네트워크 노드계산, 검색엔진 데이터베이스, 암호화, markov 체인, 컴퓨터 그래픽
- 통계(상관과 분산행렬), 심리학(요인분석과 주성분 분석), 천문학(행성 궤도 예측), 물리학(용수철 상수 표현, 좌표계측학)
- 신호처리(신호여과), 이산 fourier 변환, 수치적분, 물리학(조화운동 / 빌딩 진동 계측), 디지털 이미지 프로세서 등에 사용
▷ 컴퓨터 전공자를 위한 선형 대수학
- 우리는 3차원 공간에 살고 있으며, 이 세상의 일들을 처리하기 위해 공간을 잘 설명할 수 있는 단어가 필요함
- 컴퓨터 그래픽, 네비게이션, 게임 등이 이 방향의 대표적인 예. 선형 대수학의 무대가 되는 벡터 공간은 현실 공간의 성격을 어느 수준으로 추상화 한 것.
- 선형 대수학은 공간을 논하는데 유용한 단어와 개념을 제공해줌
- 예를 들어, "3차원 문제를 디스플레이의 2차원 평면에 어떻게 그릴것인가?"라고 생각할 때, "3차원 공간의 여기에 이런 물체가 있었던 것처럼 시각을 이런식으로 이동/회전 시키면 눈에는 어떤 2차원 이미지가 비칠 것인가?"라는 문제가 됨.
- 선형 대수를 배우는 동기는 현실 공간의 문제에 그치지 않음. 단일 숫자가 아니라 다수의 값을 쌍으로 데이터를 취급하고 싶은 장면은 거의 모든 부분에 적용됨.
▷ 선형 대수학의 응용
- 표로 표현되는 정형화된 데이터의 처리
- 흑백 영상의 표현과 처리
- 회색조영상의 표현 (0과 1사이의 값을 성분으로 갖는 행렬로 밝기의 단계 표현)
- 텍스트 데이터의 표현과 처리
↳ 단어들로 구성된 문서가 모여 있는 텍스트 데이터도 행렬로 표현 가능. 정보 검색등의 이용을 가능하게함.
- 그래프 데이터의 표현과 처리
↳ ① 쾨니히스베르크 다리 지도. ② 그래프 표현. ③ 행렬 표현
- 소셜 네트워크 데이터의 표현과 처리 (개인간의 연결 관계)
- 컴퓨터 그래픽스에서의 모델링 및 변환 (행렬 연산에 의한 물체의 이동, 카메라 위치와 방향에 따른 그림 생성)
- 로보틱스에서의 위치 결정
- 전기 회로 분석
↳ 키르히호프의 전류 법칙 (Kirchhoff's Current Law) : 어떤 교차점에 들어온 전류의 양과 나간 전류의 양의 합이 같다.
↳ 키르히호프의 전압 법칙 ( Kirchhoff's Voltage Law) : 하나의 닫힌 루프에서 전원 전압과 소비되는 전압 강하의 합은 0이다.
- 차원 축소 (고차원 공간에서 표현되는 데이터를 저차원 공간의 데이터로 변환하는 것 / 주성분 분석(PCA))
ㆍ 연립일차방정식(선형시스템)의 정의
▶ 방정식 (Equation)
- 미지수(변수)가 포함된 식에서 그 미지수에 특정한 값을 주었을 때만 성립하는 등식. 이때, 방정식을 참이되게(성립하게) 하는 특정 문자의 값을 해 또는 근이라 함
- 방정식의 해는 없을 수도 있고, 여러 개일 수도 있고, 모든 값일 수도 있음. 전자의 경우는 불능(impossible)이라 하고, 중자의 경우는 방정식, 후자의 경우는 항등식(부정, indeterminate)이라 함.
▶ 연립방정식 (Simultaneous equation)
- 방정식의 일종으로, 2개 이상의 미지수를 포함하는 방정식의 조를 연립방정식 또는 방정식계(System of equations)라고 함.
- 연립방정식은 일반적으로 대입법과 가감법을 이용해서 특정 문자들을 소거함으로써, 식을 간편화로 바꾸어서 해를 구함.
ㆍ선형시스템
- 선형 시스템(Linear system)이란 입력과 출력의 관계가 선형인 시스템을 말함
- 시스템이 선형성(Linearity)을 가지면 시스템의 출력이 입력에 대해 일관적으로 나타나므로 시스템의 특성을 해석하기 좋고 이용하기 좋음. 시스템이 비선형이면 시스템을 이해하기 어렵고 이용하기 어려워지기 때문에 공학에서는 선형 시스템을 먼저 다루어왔고, 비선형 시스템에 대한 연구도 계속 발전하고 있음
- 선형 시스템의 모든 해의 집합을 해집합이라고 함
- 선형 시스템에서 어떤 방정식들이 같은 해를 공유하면, 이를 두 식의 동치(Equivalent)라고 함.
ㆍ선형과 비선형의 특징과 차이점
| 선형 (Linear) | 비선형 (Non-linear) |
| 1차식이나 1차함수 | 1차식이 아닌 2차 이상의 함수나 cos(x) 등의 함수 |
| 하나의 원인에는 하나의 결과가 있음 | 훨씬 복잡함 |
| 그래프가 직선 | 그래프가 곡선 |
| 속도와 거리의 관계 | 카오스 등의 자연 현상 |
| 행렬로 표현 가능 | 행렬로 표현 불가 |
| 회전변환, 원점을 지나는 직선에 대한 대칭변환, 어떤 벡터공간에 대한 수직입사 등 | 피드백과 같은 복잡한 변환 |
ㆍ가우스 소거법 (Gauss elimination method)
- 선형 시스템의 해를 구하는 방법 중 하나
- 변수들을 체계적으로 소거하는 효율적인 방법이 가우스에 의해서 처음 체계화 됨
- 가우스 소거법은 주어진 선형시스템을 그것과 동치인 선형시스템으로 변화시키는 다음과 같은 3가지 연산을 필요에 따라 반복적으로 적용
① 한 방정식에 0이 아닌 상수를 곱한다.
② 방정식들의 위치를 서로 교환한다.
③ 한 방정식에 0이 아닌 상수를 곱하여 다른 방정식에 더한다.
- 가우스 소거법 과정에서 각 식의 가장 앞에 있는 0이 아닌 계수를 피벗(pivot)으로 정할 수 있다. 피벗 (성분)은 특정 계산을 수행하기 위한 임의의 알고리즘에 의해 먼저 선택된 성분이다.
ㆍ가우스-조단 소거법 (Gauss-Jordan elimination method)
- [1단계] 전향 소거법 (Forward elimination) : 각 방정식에다 다른 식의 변수의 계수를 반대가 되도록 적절한 상수를 곱하여 두식을 더함으로써 해당하는 변수들을 차례로 소거한 새로운 방정식 L을 구한다.
- [2단계] 역 대입법 (Back-substitution) : 새로운 방정식 L로부터 하나의 변수값을 구한 후 남은 식들에 차례로 대입하여 전체 해를 구한다.
ㆍ선형 대수와 선형 방정식의 생활속 응용
- 게임 이론 : 어떤 게임에서 자신에게 유리한 전략을 세우거나 자신의 이익을 극대화시킬 수 있는 여러가지 경우를 선형방정식으로 세워서 풀 수 있음.
- 경영학에서 어느 기업이 어떤 재료를 얼마만큼 사용하여 어느 정도의 양을 생산하면 최대한의 이익을 얻을 수 있는지를 선형방정식을 풀어서 응용할 수 있음. 이때 가격 책정도 선형방정식의 변수로 넣어서 풀 수 있음
- 물리학, 화학, 컴퓨터공학, 전기공학, 전자공학, 건축학, 토목학 등 여러가지 공학을 전공하는 엔지니어들에게 선형방정식의 개념과 풀이는 기초 및 응용의 바탕이 됨
- 수학을 전공하는 수학도에게는 수학을 탐구하는 굳건한 기초가 됨
- 사회 생활에서 일어나는 여러가지 복잡한 관계에서의 의사결정에 쓰임. 한정된 시간 내에 해야 할 일들의 중요성에 가중치를 두어서 선형방정식을 만들어서 해결한다.
- 천문학에의 응용 : 가우스는 팔라스 소행성을 연구하던 중 1803년부터 6년동안 행성의 궤도를 면밀히 관찰한 결과 변수가 6개인 선형방정식을 만들었으며, 그가 개발한 가우스 소거법을 이용하여 해를 구함으로써 천문학에 크게 기여함
ㆍ행렬과 행렬의 연산
- 행렬은 과학과 수학의 수많은 분야에서 다양한 응용이 있다. 물리학의 전기 회로 이론, 고전역학, 광학, 전자기학, 양자역학, 양자 전기역학 등의 분야에서 응용되며, 컴퓨터 그래픽스에서 3차원 이미지를 2차원 평면에 투영하거나 사실적인 움직임을 그려내기 위해 사용한다.
- 확률론과 통계학의 마르코프 행렬과 다변수 미적분학의 헤세 행렬 등 역시 행렬의 응용이다. 행렬 계산은 수치해석학의 중요한 문제 중 하나이다. 행렬 분해는 행렬 계산을 이론과 실제 응용에서 모두 단순화할 수 있다.
- 희소행렬, 띠행렬 등 널리 사용되는 특수한 구조의 행렬들의 경우 특화된 고속 알고리즘들이 존재한다. 천체 물리학과 양자물리학 등 분야에서는 무한 행렬도 등장한다.
▶ 행렬의 어원
- Matrix는 라틴어에서 온 영단어로, 어머니를 뜻하는 mater/matr가 어근이다. 임신한 동물이라는 의미에서 자궁이란 의미로 변화되었고, 그것이 중세기 프랑스어를 거쳐 영어에 유입되었다. 그 후, 자궁처럼 뭔가를 둘러싸고 있는 것, 즉, 조직이나 환경과 같은 뉘앙스의 여러 의미들로 확장되었다.
- 행렬은 아서 케일리와 윌리엄 로원 해밀턴이 발명했으며, '연립일차방정식의 풀이는 어떻게 하면 될까?'를 고민한데서 시작함.
- 아서 케일리의 연구 중, 행렬식의 값에 따라 연립방정식의 해가 다르게 나오는 것을 보고 이것이 해의 존재 여부, 즉 행렬의 가역 여부(invertibility)를 판별한다는 관점에서 determinant라고 부른데서 행렬식이 탄생했고, 윌리엄 로원 해밀턴이 '그러면 연립방정식의 계수랑 변수를 따로 떼어네서 쓰면 어떨까?'라는 생각에서 행렬이 탄생함. (행렬식이 행렬보다 먼저 탄생)
▶ 행렬식 (Determinant)
- 정사각 행렬에 스칼라를 대응시키는 함수의 하나
▶ 행렬 (Matrix)
- 행렬은 수 또는 문자를 배열의 형태로 나타내는 것을 말함
- 행렬의 일반적인 형태는 몇 개의 숫자들을 사각형 모양으로 배치하고 괄호를 사용하여 양 옆을 닫아놓은 형태
- m개의 행과 n개의 열을 가진 행렬을 "m x n" (m by n) 이라고 함
- 행렬안의 높은 숫자들은 행렬의 성분이라고 함
- 행렬은 A, B, C... 등 또는 [Aij], [Bij], [Cij] ... 등으로 표시함
- 1차원 행렬: 벡터(Vector)
- 행렬과 벡터의 각 원소: 스칼라(Scalar)
- 행벡터 (Row vector) : 단 하나의 행만으로 구성된 행렬
- 열벡터 (Column vector) : 단 하나의 열만으로 구성된 행렬
- Aij를 A의 (i,j)번째 원소라고 함. ( ij-항(ij-entry) 또는 ij-성분(ij-component)라고도 함 )
- n개의 행과 n개의 열을 가지는 행렬을 n차 정방행렬(Square matrix of order n)이라고 함. 이때 행의 수를 그 행렬의 차수(Order)라고 함
- A11, A22, ... Ann은 A의 주대각선(Main diagonal)상에 있다고 함
▷ 행렬의 합과 차
- 행렬의 합 : 두 행렬 A = (aij)와 B = (bij) 를 크기가 같은 m x n 행렬이라 가정. 모든 i, j에 대해서 cij = aij + bij라 할 때, m x n 행렬 C = (cij)를 A와 B의 합이라 하고 C = A + B로 표기함.
- 행렬의 덧셈은 교환법칙과 결합법칙을 만족함
↳ 교환법칙 : A + B = B + A
↳ 결합법칙 : (A + B) + C = A + (B + C)
- 행렬의 차 : 두 행렬 A = (aij)와 B = (bij) 를 크기가 같은 m x n 행렬이라 가정. 모든 i, j에 대해서 cij = aij - bij라 할 때, m x n 행렬 C = (cij)를 A와 B의 차라 하고 C = A - B로 표기함.
▷ 행렬의 스칼라 곱셈
- k가 실수 값이고, A = [aij]를 임의의 행렬이라고 할 때, kA는 ij-성분이 kaij인 행렬로 정의되므로 kA = [kaij]이다. 즉, 행렬 A에 스칼라 값 k를 곱했을때 k x A는 행렬 A의 각 항에다 k를 곱함으로써 얻어짐.
- 행렬들의 곱셈에서는 교환법칙이 성립하지 않음. (AB != BA)
- A가 m x n 행렬이고, B와 C는 행렬의 합과 곱에서 정의된 크기를 만족한다고 가정, k가 어떤 스칼라 값일때 다음의 식들이 성립함
↳ 곱셈의 결합법칙 : A(BC) = (AB)C
↳ 왼쪽 배분법칙 : A(B+C) = AB + AC
↳ 오른쪽 배분법칙 : (B+C)A = BA + BC
↳ 스칼라 곱 : k(AB) = (kA)B = A(kB)
↳ 행렬 곱셈의 항등식 = InA = A = AIn
▷ 열벡터의 선형 결합에 의한 행렬 곱 계산
- 다른 방식으로 행렬의 곱을 이해하는 방법
- 오른쪽에 곱해지는 행렬의 한 열만 가져와서 결과 확인
> 벡터 간의 선형 결합 (Linear combination) = 상수 x 벡터[] 의 합을 조합해 표현한 것
▶ 블록 행렬 (분할 행렬)
- n x n 행렬 = (n/2) x (n/2) 부행렬의 2 x 2 행렬
- 행렬계산의 고속화 (병렬처리)
▶ 특수한 형태의 행렬
- 정방행렬 A의 주대각선 위의 모든 성분들을 대각항이라고 하고, 각 대각항의 합을 대각합(trace)이라고 하며 tr(A) 또는 trace(A)로 표기함.(행과 열 번호가 같은 성분들의 합). 고유치/고유벡터 쓸때 사용
- A와 B가 같은 크기의 정방행렬일때 대각합은 아래의 특성을 가짐
↳ tr(A^T) = tr(A)
↳ tr(cA) = ctr(A)
↳ tr(A+B) = tr(A) + tr(B)
↳ tr(A-B) = tr(A) - tr(B)
↳ tr(AB) = tr(BA)
- 대각행렬이면서 대각선의 항들이 모두 1인 n x n 행렬을 항등행렬(Identity matrix) 또는 단위행렬이라고 함.
- 행렬의 크기가 n x n인 항등행렬을 통상 In으로 나타내는데, 문맥상 행렬의 크기가 분명할 경우 그냥 I로 나타내기도 함.
- 성분이 모두 0인 행렬, 즉 모든 i, j에 대하여 aij = 0인 행렬을 영행렬(zero matrix)라고 함.
- 전치행렬 = 행과 열을 바꿈
- A = - A^T 를 만족하는 n x n 행렬을 교대행렬(Skewed-symmetric matrix)이라고 함
- 주대각선 아래에 있는 모든 항들이 0인 n x n 행렬 A를 상부삼각행렬(Upper triangular matrix)이라 하며, 반대로 주대각선 위의 모든 항들이 0인 행렬은 하부삼각행렬(Lower triangular matrix)이라고 함. 통칭하여 삼각행렬(Triangular matrix)이라고 함.
▷ 주성분 (Pivot)
- 행렬의 영벡터가 아닌 행에서 0이 아닌 좌로부터의 최초의 성분은 그 행의 주성분(pivot)이라고 함.
▷행사다리꼴행렬 (Row echelon form matrix)
- 성분이 계단모양으로 배열된 행렬
- 0으로만 이루어진 행들은, 만약 있는 경우, 행렬의 아래쪽에 나타냄
- 모두가 0이 아닌 행의 가장 왼쪽에 가장 처음 나타나는 0이 아닌 수를 피벗으로 삼는다.
- 모두가 0이 아닌 연이은 두 행이 있으면 아래쪽 행의 피벗은 위쪽 행의 피벗보다 오른쪽에 있다.
▷ 기약 행 사다리꼴 행렬 (Reduced row echelon form)의 정의
- 행 사다리꼴에서 행의 처음이 숫자가 0이 아닌 1. (= 선행 1)
- 선행 1이 속한 열의 나머지 성분은 모두 0
↳ 피벗의 위와 아래의 숫자가 모두 0.
> 행렬의 기본 연산과 사다리꼴
- 기본 행 연산에서 전향단계만 거치면 가우스 소거법이고, 후향단계까지 거치는 것을 가우스-조단 소거법이라고 함.
- 가우스 소거법은 행 사다리꼴을 만들어내고, 가우스-조단 소거법은 기약 행 사다리꼴을 만들어냄.
- 주어진 행렬을 행 사다리꼴로 만들었을때 행 전체가 0이 아닌 행의 개수는 수학적으로 중요한 의미를 가지는데, 이 수를 주어진 행렬의 계수(Rank)라고 함.
- Rank라는 것은 어떤 행렬을 소거했을때 만들어지는 pivot의 개수를 의미하며 행렬이 표현할 수 있는 차원(Dimension)을 의미하기도 함.
- Rank는 m by n 크기의 행렬에서 반드시 m 보다 작거나 같고, n 보다 작거나 같음.
ㆍ행렬식
- 행렬식(Determinant)은 정방행렬 A를 실수값으로 대응시키는 함수로, det(A) 또는 |A|로 표기한다.
- 행렬식은 역행렬이 존재하지 않으면 0, 그렇지 않으면 0이 아닌 값을 가진다.
- 행렬의 특징을 나타내는 지표의 하나, 스칼라 값을 가짐.
- 행렬식이 가장 활약하는 곳은 역행렬 도출할 때
- 행렬식은 정방행렬에 대해서만 정의됨
▶ 행렬식이 활용되는 대표적인 사례
- 행렬식은 행렬 A가 가역행렬인지 판별함. 즉, 역행렬 A^-1가 존재하는지 판별
- 행렬 A를 이용하여 선형변환을 할 때, 넓이 또는 부피의 변화율을 계산함
- 행렬식을 활용하여 역행렬 계산
- 행렬식으로 연립선형방정식의 해를 구함
- 행렬식으로 행렬의 고윳값과 고유벡터 계산
▶ 여인수 전개 (Cofactor expansion)
- 여인수란 어떤 행렬의 행과 열을 하나씩 제외시켜 남은 행렬의 행렬식에 +, - 부호를 붙인 것
- 행렬식은 행 또는 열에 대한 "성분 x 여인수" 끼리의 합의 형태로 전개됨
- n x n 정방행렬 A의 행렬식 |A|의 값이 0이 아닐때 A를 정칙행렬(Non-singular matrix)이라고 하고, |A| = 0일 때, A를 특이행렬(Singular matrix)이라고 함.
- Aij = (-1)^i+j * Mij

▷ 소행렬(Minor matrix)식
- 한 행렬식에서 어느 한 원소의 소행렬식은 그 원소가 위치한 행과 열을 제외시킨 행렬식을 말함.
- A를 n x n 삼각행렬(상부or하부삼각행렬)이라고 하면, Det(A)는 주대각선상의 원소들인 a11, a22, a33, ... ann을 모두 곱한 값과 일치한다. (삼각행렬이 가역적(Invertible)이기 위한 필요충분조건은 그 대각선상의 모든 성분들이 0이 아니어야 함)
↳ Det(A) = a11 x a22 x ... x ann
> 여러번의 기본 행 연산을 통하여 행 사다리꼴로 만든 후 주대각선상에 있는 원소들을 곱하기만 하면 행렬식의 값을 쉽게 구할 수 있음.
> 행 교환시 부호 바뀜
ㆍ역행렬 (Inverse matrix)
- A를 정방행렬이라고 하고, I를 같은 크기의 단위행렬이라고 할 때, A^-1이 존재한다면 이를 A의 역행렬이라고 한다.
↳ A*A^-1 = A^-1*A = I
↳ (A^-1)^-1 = A
↳ (AB)^-1 = B^-1*A^-1
- 가역적(Invertible) = 역행렬을 구할 수 있을 경우를 말함
> 역행렬을 구하는 방법
- 가우스-조단 방법
↳ 1. 원래의 A 행렬에다 항등행렬 I를 첨가하여 첨가행렬 [A | I]로 만든다.
↳ 2. 행렬 A 부분이 항등행렬로 바뀔때까지 행 연산을 계속한다.
↳ 3. A가 가역적 행렬인지 결정한다.
- 한 행렬을 변수로 놓고 곱을 구해서 항등행렬이 되도록 하는 방법
- 수반행렬을 이용하여 구하는 방법
↳ A의 여인수를 성분으로 가지는 행렬 C = [Aij]를 행렬 A의 여인수 행렬이라고 할 때 여인수 행렬 C의 전치행렬(행과 열의 위치를 바꾼행렬)을 A의 수반행렬(Adjugate matrix)이라고 하며 Adj(A)와 같이 나타낸다.
▷ 첨가행렬 (Augmented matrix)
- 주어진 행렬 A의 오른쪽에다 추가적으로 첨가하여 만든 행렬
ㆍ연립선형방정식
- 특정 미지수에 대한 선형방정식들이 모여 있는 것을 연립선형방정식 또는 선형시스템이라고 한다.
- 행렬과 연립선형방정식과는 밀접한 관계가 있음.
- 선형방정식 = 일차방정식
- 같은 미지수에 대하여, 두 연립선형방정식이 동일한 해집합을 가지면, 두 연립선형방정식은 동치라고 한다.
- Ax = b가 n개의 변수에 대한 n개의 방정식으로 이루어진 선형시스템이고, 행렬 A가 가역적이면 선형시스템은 유일한 해 x = A^-1*b를 가진다.
▶ 해집합 (Solution set)
- 연립선형방정식의 해를 모아놓은 집합
- 해 : 연립선형방정식의 모든 방정식을 만족하는 미지수의 값
▶ 행렬방정식 (Matrix equation)
- 연립선형방정식을 행렬과 벡터의 곱으로 Ax = b와 같이 표현한 것
▷ 연립선형방정식의 풀이법
> 동치인 연립선형방정식을 만드는 연산과 행렬방정식의 행 연산
- 두 선형방정식의 위치를 교환하는 것은 행렬방정식의 계수행렬과 상수벡터에서 대응하는 두 행을 교환하는 것과 같다.
- 선형방정식의 양변에 0이 아닌 상수를 곱하는 것은 행렬방정식의 계수행렬과 상수벡터에서 대응하는 행에 해당 상수를 곱하는 것과 같다.
- 특정 선형방정식의 0이 아닌 상수배를 다른 선형방정식에 더하는 것은 행렬방정식의 계수행렬과 상수벡터에서 대응하는 한 행의 상수배를 다른 행에 더하는 것과 같다.
▶ 크래머의 규칙
- 유일한 해를 가지며 변수와 방정식의 수가 같은 연립일차방정식의 해를 구하는 공식.
- 계수 행렬과 그 한 열을 상수항으로 대신하여 얻는 행렬들의 행렬식의 비를 통해 해를 나타냄
▶ LU 분해법 (L=Lower, U=Upper)
- 주어진 행렬 A에 대해서 A를 하삼각행렬 L과 상삼각행렬 U와의 행렬의 곱으로 나타낸 것
- Doolittle 분해 = [L]의 대각요소를 1이 되도록 분해하는 방법
- Crout 분해 = [U]의 대각요소를 1이 되도록 분해하는 방법


ㆍ벡터의 개념과 표현
- 다수의 수치를 조합한 데이터를 다루고 싶은 장면은 무엇을 하든 나올 것. 이때, 데이터를 단지 "수치의 쌍"으로서 취급하는 것이 아니라 "공간내의 점"으로 간주하는 것으로의 직관을 활용하자라고 하는 것이 중요한 관점이다.
| 자면 (겉으로 드러난 문자의 의미) | 의미 | |
| 벡터 | 숫자를 일렬로 나열한 것 | 화살표 또는 공간상의 점 |
| 행렬 | 숫자를 장방형으로 나열한 것 | 공간으로부터 공간으로의 사상 |
| 행렬식 | 매우 복잡한 계산 결과 | 위의 사상에 따른 체적확대비율 |
- 압력, 속력, 물체의 질량, 전자의 저하, 물의 비열, 저항기의 저항, 원의 지름, 삼각형의 면적, 육면체의 체적 등과 같은 물리적 양은 주어진 양의 크기인 실수로 표현할 수 있다. 이때 실수 값을 스칼라라고 한다.
- 단 하나의 수만으로는 나타낼 수 없는 또 다른 물리적 및 기하학적 양도 있는데, 속도, 힘 그리고 가속도 등은 그들의 크기 뿐만 아니라 방향까지도 포함된다. 이러한 것들을 벡터라고 한다.
- 물리학에서 벡터는 방향을 나타내는 물리량이다. 그들에게 벡터는 방향과 크기만 같으면 어디에 있든 같다.
- 컴퓨터 과학에서 벡터는 순차리스트이다. 이들은 벡터를 이용하여 여러가지 데이터를 모델링한다.
- 수학에서 벡터는 이들 모두를 포함하는 개념으로 (벡터합, 스칼라곱)이라는 개념이 성립하면 벡터이다.
- 벡터의 시작점을 시점(Initial point, tail), 끝나는 점을 종점(Terminal point, head)라고 함.
- 시점에서 종점까지의 방향을 가진 선분을 유향선분(Directed segment)이라고 함.
- Vector 라는 단어는 '전송'을 나타내는 라틴어 vect로부터 나옴.
- Scalar의 어원은 스케일(크기)로, 눈금의 숫자만 표현할 수 있음
▷ 위치벡터 (Position vector)
- 3차원 공간에서 원점 (0,0,0)으로부터 좌표상의 위치 (x, y, z)까지 향하는 벡터
- 벡터의 시점은 평면 또는 공간의 어떠한 점을 잡아도 좋으나 보통 원점으로 잡음
- 시점을 고정하지 않은 벡터를 자유벡터 (Free vector)라고 함
- 두개의 벡터가 대응하는 각 성분(크기, 방향)이 같으면 두 벡터는 동치 또는 상등이라고 함.
- 벡터의 시점과 종점의 위치에 관계없이 크기와 방향만을 생각할때 이를 기하벡터(Geometric vector)라고 함.
- 벡터의 크기는 피타고라스 방정식으로 풀수 있음.
▷ 단위벡터 (Unit vector)
- 어떤 벡터의 단위벡터는 "방향이 변하지 않고 강제적으로 크기가 1로 변환된 벡터이다
- 단위벡터는 반드시 반경이 1인 원(2차원), 구(3차원) 상에 있다.
- 단위벡터를 사용하면 벡터를 크기와 방향으로 나누어서 표현할 수 있다.
▷ 단위좌표벡터 (Unit coordinate vector)
- 다른 벡터들을 편리하게 나타낼 수 있는 두 개의 특별한 벡터
- 두 벡터를 벡터공간의 기저벡터라고 한다.
- 선형대수학에서, 어떤 벡터 공간의 기저(basis)는 그 벡터 공간을 선형생성하는 선형독립인 벡터들이다. 달리 말해, 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터들이다.
> 벡터의 생활속 응용
- 물리학에서 두 물체 사이의 이동이나 상호작용을 나타내는 척도로 매우 중요한 역할을 한다.
- 일이나 에너지같은 물리량을 벡터로 나타내어 복잡한 연산을 간편하게 한다.
- 자연법칙을 수식으로 표현할 때는 물리량에 의해 가능한데, 이것을 벡터와 스칼라를 통해 나타낼 수 있다.
- 네트워크를 분석하거나 경로 탐색 등에 중요한 역할을 한다.
- 컴퓨터 그래픽에 응용될 수 있다.
▶ 직교 좌표계
- 서로 직각을 향하고, 길이가 같은 벡터 3개로 구성된 좌표계. (길이가 1이고 서로 수직)
- 좌표라는 개념은 벡터를 연결한 것이다.
ㆍ벡터공간과 선형독립
- 벡터공간(선형공간)이란 벡터와 같은 성질을 갖는 요소들의 집합이며, 집합 중에서도 특정 조건을 만족하면 벡터공간이라고 한다.
- 집합은 유한이든 무한이든 상관없으며, 정수와 같은 무한개의 집합도 조건 만족시 벡터공간에 해당한다.
- 집합은 V라는 기호로 표현한다.
- 어떤 집합 V가 벡터공간인지 여부를 생각하는데 있어서 두가지의 연산 규칙(덧셈과 스칼라 곱)이 포함되어 있다고 전제한다.
↳ 덧셈 : 집합 V에 어떤 임의의 2개 요소 a와 b를 주어져 있다고 할 때, "a+b"를 나타낼 수 있는 V 내의 요소를 결정할 연산이다.
↳ 스칼라 배 : 실수 집합 또는 복소수 집합 안에 있는 스칼라 값
↳ 덧셈과 스칼라 곱이 다음 7가지 조건을 만족해야 한다.
(1. 덧셈의 교환법칙, 2. 덧셈의 결합법칙, 3. 역벡터의 존재, 4. 덧셈의 역원, 5. 스칼라 곱의 결합법칙, 6. 스칼라 곱에서 스칼라 분배법칙, 7. 스칼라 곱에서 벡터(요소)의 분배법칙)
- "방향과 크기"를 나타내는 존재였던 벡터가 "일정하게 정해진 수의 배열"이라고 하는 개념으로 확장되고, 두 원소를 더하거나 주어진 원소를 임의의 실수배 만큼 자유롭게 늘이거나 줄이는 것이 가능한 집합으로서 개념 추상화됨.
- 벡터공간은 실벡터공간(Real vector space)과 복소벡터공간(Complex vector space) 두가지로 나누어짐.
↳ 실벡터공간(실선형공간) : 스칼라로서 실수가 사용된다고 전제하는 경우
↳ 복소벡터공간(복소선형공간) : 스칼라로서 복소수가 사용된다고 전제하는 경우
▷ 영벡터공간 (Zero vector space)
- 영벡터 0 하나만으로 구성되는 벡터 공간
▷ 부분공간 (Sub space)
- 어떤 벡터공간 V에서 적당한 벡터를 모아서 부분 집합 W를 만들어보면 W 집합 자신도 벡터 공간이다라는 것을 알 수 있다. 여기서 W를 V의 부분공간이라고 한다.
- W가 V의 부분공간인 조건은 W가 공집합이 아니고, 또한 V의 연산 규칙이 W상에서 벡터공간의 7개 조건을 충족하는 것.
- 간단히 말하면, W의 모든 벡터를 연산했을 때, 그 결과가 항상 W에 있으면 W는 부분공간이다.
▶ 선형독립 (1차독립)
- 선형독립은 다수의 벡터로 구성된 그룹에 대해서, 어떤 벡터가 다른 벡터의 실수배와 그 합으로 나타낼 수 없는 상태를 말한다.
- 선형독립의 반대에 해당하는 상태가 선형종속(1차종속)이다. 즉, 어느 벡터가 다른 벡터의 실수배와 그 합으로 나타낼 수 있는 상태이다. 또한 벡터에 다른 벡터의 실수배와 그의 합으로 나타낸 것을 선형결합(1치결합)이라고 한다.
▷ 기저 (Basis)
- xy 평면에 있어서 "x축 벡터와 y축 벡터"라는 조합을, 벡터 공간의 세계에서는 기저라고 한다.
- 선형독립이며 선형생성의 조건을 가진다.
▷ 차원 (Dimension)
- 벡터공간 V의 기저를 구성하는 벡터의 개수
- dimV로 표현
ㆍ고유값과 고유벡터 (Eigenvalue & Eigenvector)
- 선형대수에서는 어떤 벡터 x에 대해서 정방행렬 A를 왼쪽에 곱해서 다른 별도의 벡터로 변환하는 방법이 자주 사용된다. (이를 행렬 A에 의한 선형변환이라고 함)
- 선형변환을 하면 거의 모든 벡터는 행렬 A와의 행렬곱에 기초해서 다른 별도의 벡터로 변화한다. 그러나 그 중에서 벡터의 크기만 변할 뿐 방향은 일절 변화가 생기지 않는 벡터가 존재하는 경우가 있다. (즉, 벡터 Ax가 같은 벡터 x의 스칼라 배의 형태로 표현할 수 있음)
- 방향이 변하지 않는 특별한 벡터 x를 고유벡터라 하고, 변환 후에 있어서 벡터의 크기의 변화를 고유값이라 한다.
- 고유값과 고유벡터는 쌍으로 되어있어, 어떤 행렬 A에 대해서 여러가지의 고유값과 고유벡터의 쌍이 있는 경우가 대부분이고, x가 영벡터이면 어떤 경우에도 성립하기 때문에 영벡터는 고유벡터로 취급하지 않음.
- 고유값과 고유벡터는 어떤 행렬을 이용한 선형변환의 특징을 나타내는 지표 중 하나
- 선형대수에서 학습하는 고유값과 고유벡터는 일상생활에서 많이 사용됨 (ex. Google의 PageRank 검색엔진 알고리즘, 주성분 분석 통계학, 양자역학 - 시간에 의존하지 않는 슈뢰딩거 방정식)
> 고유값과 고유벡터를 구하는 방법 → 고유방정식(특성방정식)
① 고유방정식을 풀어서 고유값을 유도
② 고유값에 대한 고유벡터를 유도
- 고유벡터는 하나의 고유값에 대해서 무수히 있을 수 있음 (어떤해의 스칼라 배도 해가 되기 때문에). → 고유값 벡터를 구하는 문제에 대해서 특별한 내용이 없는 한 임의의 변수를 스칼라 배한 형태로 기술함.
▶ 대각합과 고유다항식
- 대각합(Trace) : 정방행렬의 대각성분의 총합을 의미함
- 고유다항식의 좌변을 의미함
- A가 n차 정방행렬인 경우 고유다항식은 n차 정방행렬의 행렬식이므로, 고유 방정식은 람다에 관한 n차 방정식이다.
- 고유방정식의 해는 행렬 A의 고유값이다. 고유다항식은 고유값으로 인수 분해 가능.
> 대각합과 고유값 사이의 관계
- 고유방정식을 "행렬의 성분을 이용한 표현"과 "행렬의 고유값을 이용한 표현" 두 종류로 표현할 수 있다는 것은 양쪽 변수의 계수를 비교하므로서 성분과 고유값 사이에 일정한 관계를 찾아낼 수 있다는 것.
- 행렬 A의 대각합과 A의 고유값의 합은 같다.
> 행렬식과 고유값 사이의 관계
- 행렬 A의 행렬식은 A의 고유값의 곱으로 나타낼 수 있다.
▷ 행렬의 대각화
- 어떤 정방행렬 A에 대해서 적절한 정칙 행렬 P를 이용해서 P^-1*AP가 대각 행렬이 될 수 있다.
- 대각 행렬을 만드는 과정을 대각화라 하고, 대각화 할 수 있는 P가 존재하는 것을 대각화 가능이라고 함.
- 대각화의 이점 중 하나는 행렬의 n승 계산에 유용하다는 것. 대각 행렬의 n승은 원래의 대각 성분의 n승을 성분으로 갖는 대각 행렬이 된다.
- 대각화 가능 조건 = 1.고유값을 구한다. 2.대응하는 고유벡터를 구한다. 3.차수와 동일한 수의 고유벡터가 서로 1차독립인지 알아본다.
▶ 대칭행렬
- 행렬의 대각 성분을 축으로 우상과 좌하가 대칭으로 되어 있는 정방행렬
- 전치(Transpose)해도 변하지 않는 행렬
- 실수만을 성분으로서 가지는 행렬을 특히 실대칭 행렬이라고 함
▶ 직교행렬
- 전치와의 곱이 행렬 E가 되는 행렬. 즉, 전치가 역행렬 그 자체인 행렬을 말함.
- 고유값이 모두 실수인 행렬은 삼각화 가능 (직교행렬 이용)
- 삼각화란, 대각 성분의 좌하(혹은 우상)가 모두 0이 되는 행렬을 만드는 작업을 말함
- 삼각 행렬을 포함하는 수식은 계산이 편하고 선형대수를 실용하는데 중요한 역할을 함
▷ 유니터리 행렬 (Unitary)
- 정방 행렬의 고유값 중에 복소수가 포함되는 경우, 유니터리 행렬로 삼각화 할 수 있다.
- 복소수 버전의 직교 행렬같은 존재. 어느 행렬을 전치하여 모든 성분을 컬레 복소수(허수 부분의 부호를 바꾼 복소수)로 옮겨서 행한 행렬(수반 행렬)이 어느 행렬의 역행렬이 되는 행렬.
> 삼각화의 방법
1. 고유값 및 고유벡터를 구한다
2. 특정 고유 벡터와 직교한 벡터를 모은다
3. 벡터 크기를 1로 정렬한다
4. 오른쪽 상단을 제외한 소행렬에 동일한 작업을 수행한다
5. 모든 P를 곱한다
▷ 고유값과 고유벡터의 생활속의 응용
- 고유값은 선형변환의 대각화에 매우 중요한 개념을 제공
- 물리적인 시스템의 중요한 특성을 표현하는 수학적 모델의 개발에 유용함
- 행렬의 거듭제곱의 계산에 고유값의 개념을 도입하면 매우 편리함
- 인구 증가 모델의 분석과 동역학 분석에 유용함
ㆍ선형변환 (Linear transformation)
- 선형성을 갖는 f가 입력된 값을 별도 값으로 출력하는 것.
- 본질적으로 변환 f는, 함수(Function), 사상(Mapping)의 동의어이다.
- 선형변환의 특징 3가지
(① 변환전이나 변환 후에도 직선은 직선 그대로 ② 변환전이나 변환 후에도 원점은 변환없이 고정 ③ 모든 직선은 평행하고 등간격 유지)
- 변환행렬이란 기저벡터의 목적지를 지정하는 것
- 2차원 공간의 선형변환은 4개의 숫자를 파악하는 것으로 완전히 이해가능. 4개의 숫자는 기저 벡터 i의 목적지를 나타내는 2개의 숫자와 j의 목적지를 나타내는 2개의 숫자.
- 행렬이란 이 네개의 숫자를 결합한 것에 지나지 않음. (즉, 행렬이란 단순히 기저 벡터의 목적지를 지시하는 것에 지나지 않음)
- 대표적인 선형변환 행렬 종류 : 반전행렬, 회전행렬, 신장행렬, 압축행렬, 사영(투영)행렬, 전단행렬

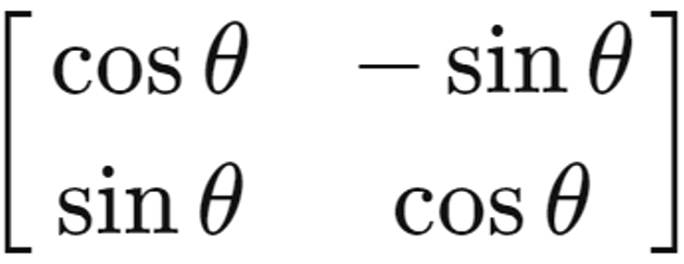



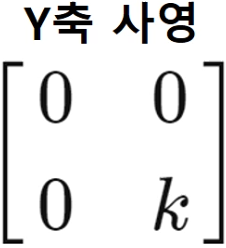
- 사형변환은 수직으로 태양 빛에 그림자가 만들어지는 변환

- 전단행렬이란 i 혹은 j 중 어느 한쪽으로 그대로 두고 그중 한쪽의 기저벡터의 0쪽 요소만을 변환하는 것
▶ 선형사상 (Linear map)
- 1변수끼리 또는 다변수끼리의 대응 관계
- 1차 함수(직선 방정식)도 선형 사상의 일종.
- 벡터 공간간의 덧셈과 정수배가 만족하는 사상
▷ 선형변환의 생활속 응용
- 선형변환은 선형 관계에 있는 다양한 데이터들의 변화에 따른 처리를 매우 원활하게 하여, 빠르고 정확한 계산을 가능하게 한다.
- 데이터의 단순화를 통하여 더욱 간편하게 각종 통계적 처리를 할 수 있도록 해준다.
- 선형변환은 높은 차원의 벡터를 사영을 통하여 낮은 차원의 벡터로 변환시켜준다.
- 응용의 폭이 매우 넓은 행렬에서의 선형변환을 통하여 수학, 물리학, 공학 등에 많이 활용된다.
- 컴퓨터 그래픽에서 선형변환을 통해 점이나 도형 등의 영상을 변환시켜서 처리할 수 있으며, 다양한 그래픽의 변화를 통해 우리 눈을 즐겁게 해준다.
댓글